
알고리즘 분류
- 그래프 이론
- 자료 구조
- 분할 정복
- 분리 집합
- 오프라인 쿼리
- 오프라인 동적 연결성 판정
문제
N개의 정점으로 이루어진 루트없는 트리의 포레스트 F가 있다. 가장 처음에 F에 속하는 모든 트리는 정점 하나로만 이루어져 있는 트리이다. 아래와 같은 쿼리를 수행해보자.
- 1 A B: 정점 A와 B를 연결하는 간선을 추가한다. 쿼리가 주어지기 전에 A와 B사이에는 간선이 없다.
- 2 A B: 정점 A와 B를 연결하는 간선을 제거한다. 쿼리가 주어지기 전에 A와 B사이에는 간선이 있다.
- 3 A B: 정점 A에서 B로 가는 경로가 있는지 없는지 조사한다. 있는 경우에는 1, 없는 경우에는 0을 출력한다.
모든 A와 B는 1 ≤ A, B ≤ N, A ≠ B를 만족하고, 모든 간선은 방향이 없다.
입력
첫째 줄에 정점의 개수 N(2 ≤ N ≤ 100,000)과 쿼리의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에 쿼리가 한 줄에 하나씩 주어진다. 쿼리의 수행 결과가 포레스트인 입력만 주어진다.
출력
3번 쿼리의 결과를 한 줄에 하나씩 출력한다.
#include <iostream>
using namespace std;
int N, M, root;
int *arr;
void setN(int N) {
arr = (int *)malloc(sizeof(int) * (N + 1));
for (int i = 0; i < N + 1; i++) {
arr[i] = i;
}
}
void unionFind(int a, int b) {
if (arr[b] != b) {
do {
root = arr[b];
arr[b] = a;
a = b;
b = root;
} while (arr[root] != root);
arr[root] = a;
}
else arr[b] = a;
}
void del(int a, int b) {
if (a == arr[b]) {
arr[b] = b;
}
else {
arr[a] = a;
}
}
bool connection(int a, int b) {
while (arr[a] != a) {
a = arr[a];
}
while (arr[b] != b) {
b = arr[b];
}
if (arr[a] == arr[b]) return true;
else return false;
}
int main(void) {
cin >> N >> M;
int q, a, b, l;
setN(N);
for (int i = 0; i < M; i++) {
cin >> q >> a >> b;
if (q == 1) {
unionFind(a, b);
}
else if (q == 2) {
del(a, b);
}
else if (q == 3) {
l = connection(a, b);
cout << l << endl;
}
}
free(arr);
return 0;
}setN 함수 : 각 정점이 어떤 정점과 연결되어 있는지 알려주는 크기 N+1의 동적 배열을 초기화하는 함수
void setN(int N) {
arr = (int *)malloc(sizeof(int) * (N + 1));
for (int i = 0; i < N + 1; i++) {
arr[i] = i;
}
}

for (int i = 0; i < M; i++) {
cin >> q >> a >> b;
if (q == 1) {
unionFind(a, b);
}
else if (q == 2) {
del(a, b);
}
else if (q == 3) {
l = connection(a, b);
cout << l << endl;
}
}
그 다음 for문을 통해 쿼리 q와 정점 넘버 a, b를 M번 입력 받도록 했습니다.
안에서는 if문을 통해 알맞은 수행을 할 수 있는 함수를 호출해줬어요.
unionFind 함수 : 정점끼리 연결하는 간선을 추가해주는 함수
void unionFind(int a, int b) {
if (arr[b] != b) {
do {
root = arr[b];
arr[b] = a;
a = b;
b = root;
} while (arr[root] != root);
arr[root] = a;
}
else arr[b] = a;
}
main문에서 입력 받은 정점 2개를 매개변수로 함수에 전달해줍니다.
정점 b가 아직 연결된 간선이 없을 경우에는 그대로 배열 arr[b]에 a 값을 주어 a와 b가 연결됐음을 표시하려 했습니다.
다만, b가 이미 다른 정점과 연결이 돼 있어서 arr[b] = b 가 아니라면 기존에 b랑 연결되어 있던 정점 번호를 root로 기록하고 arr[b]에는 새로 연결된 정점의 번호를 부여했습니다. 이 과정을 연결된 간선이 없는 정점을 만날 때까지 반복해줬습니다. 그러면 각 배열에 빠짐 없이 연결된 각 정점의 번호가 저장이 됩니다.
예시를 보여 드릴게요
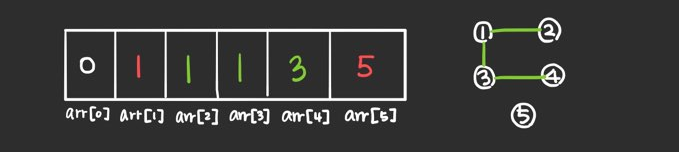
문제에서 주어진 예시대로 1 1 2 / 1 1 3 / 1 3 4 를 입력 받고 나서의 상태입니다.
처음에 2는 연결된 정점이 없기 때문에, 즉 arr[2] = 2이기 때문에 else 로 들어가서 arr[2] = 1 이 됩니다.
정점 3과 4도 마찬가지로 arr[i] = i 꼴이기 때문에 각각 1과 3 값을 가지게 됩니다.
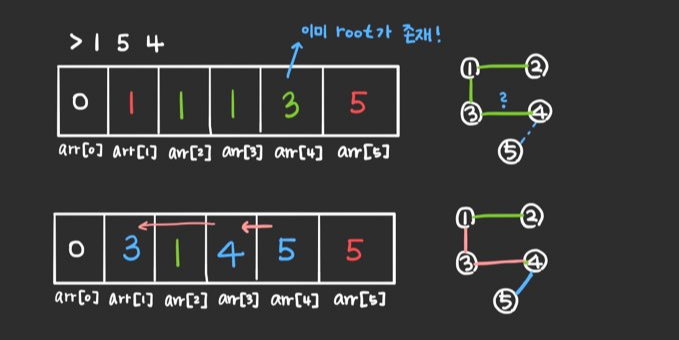
문제는 그 다음 입력값으로 1 5 4 를 받았을 때입니다.
arr[4] = 3 으로 정점 4는 이미 정점 3과 연결이 된 상태입니다.
여기서 그냥 arr[4] = 5로 값을 주게 되면 나중에 3과 4가 연결되어 있는지 추적할 때, 찾을 방법이 없어지게 됩니다.
그래서 우선 변수 root 에 이전에 4와 연결된 정점 3의 값을 저장합니다. 그 다음 arr[4] = 5 로 4와 5가 연결됐음을 나타내고, 순서대로 a = b; , b=root; a는 4가 되고 b는 3이 됩니다. 여전히 arr[3] != 3 이므로 이 과정을 반복해주면(연결된 정점이 없는 정점 1을 만날 때까지) 결과적으로 모든 배열에 중복되지 않고 연결된 정점들이 기록되게 됩니다.
del 함수 : 연결되어 있는 간선을 삭제하는 함수
void del(int a, int b) {
if (a == arr[b]) {
arr[b] = b;
}
else {
arr[a] = a;
}
}
정점 a와 b는 이미 연결되어 있는 상태이기 때문에 적어도 arr[a] = b 이거나 arr[b] = a인 상태일 겁니다.
두 정점 사이의 간선을 끊는 것이기 때문에 arr[b] == a이면 arr[b]에 b의 값을 주어 더 이상 두 정점을 연결하는 선이 없음을 나타내면 되고, 반대일 경우 반대로 하면 됩니다.
connection 함수 : 두 정점 간의 연결성을 확인하는 함수
bool connection(int a, int b) {
while (arr[a] != a) {
a = arr[a];
}
while (arr[b] != b) {
b = arr[b];
}
if (arr[a] == arr[b]) return true;
else return false;
}
문제에서 쿼리 q=3일 경우에 출력값을 가지므로 connection 함수는 return 값을 가지는 bool 함수입니다.
두 정점 사이의 연결을 확인하기 위해서는 단순히 각 배열에 저장된 값만 비교해서는 안 됩니다.

예를 들어 볼게요.
1과 4는 직접적으로 간선을 연결하진 않았지만 정점 3으로 인해 연결되어 있습니다.
그런데 arr[1] = 1이고 arr[4] = 3이기 때문에 이것만 가지고는 1과 4의 연결을 확인할 길이 없습니다.
따라서 각 a와 b의 최상위 정점을 찾아가야 합니다. arr[1] = 1이기 때문에 더 이상 이동할 곳이 없네요.
그러나, arr[4] = 3이라 정점 3으로 이동해서 정점 3은 어느 정점이랑 연결되어 있는지 확인해 볼 수 있습니다.
arr[3] = 1 이므로 1이랑 연결이 되어 있네요.
따라서 4는 3이랑 연결되어 있고 3은 1이랑 연결되어 있으니 4는 1과 연결되었음을 확인할 수 있습니다. 이를 구현해서 최상위 정점이 같으면 true 값을, 다르면 false 값을 반환하도록 했습니다.
마지막으로 동적배열의 메모리 해제를 해주면 코드가 마무리됩니다!
아직 부족한 부분이 많습니다
궁금하신 점이나 오류 발견하신 분들은 알려주시면 감사하겠습니다 :-)
'Algorithm > 백준' 카테고리의 다른 글
| 백준 17968 : Fire on Field (0) | 2020.11.05 |
|---|

